重构的七宗罪
重构经过了十几年的发展和应用,可以说它是极限编程中程序员最爱的实践之一了,纷纷争相在项目里应用。重构工作坊、Codekata重构练习等各种提升能力的方式也屡见不鲜,帮助程序员们去追求优秀的代码和设计。然而这仍然摆脱不了人们对它的各种抱怨:“搞什么,又重构”,“重构出defect来了”,“项目紧,最近不要再重构了”,“重构到什么时候停呀”。小菜也这样被项目中的人抱怨着,觉得很委屈,找到了大牛小明。
小菜:有一大段代码不合我意,写的很烂。我就想最近刚好新学了点技巧,看了下模式,赶紧大干一场。没想到做着做着组里都反对。
小明:那你有什么目标?重构想达到什么效果?
小菜:目标?啥意思?
小明:我们做事情得有目标,重构任务也是一样的。
小菜:我不太清楚,我就是想把这段代码改了,我删了好多代码,测试好多都红了。项目好像下周发布,项目经理小东也问我什么时候完工;测试小花还说我前两天做的功能有问题,问我是不是又重构了;
小明:你呀,今天来对了。这两天我也在琢磨这个戏,重构七宗罪,正好给你来讲一下。
1.不懂重构,为了重构而重构
“没有目标而生活,恰如没有罗盘而航行。”
做事情得有一个目标,拿出租车举例:“师傅,我要去机场”。出租车师傅很清楚我们的目的地。然如果我们说,“师傅,我就是来坐车的,你随便开吧”,就是再有经验的司机也没办法把你送到终点。重构也是一样,它需要能够解决一定的问题,要有一个目标的引领,否则黑咕隆咚做了半天也不知道自己做了啥,最后不得不全部回滚,白费工夫。
那么重构是什么,它解决什么问题呢?
所谓重构是对软件内部代码及其结构的调整,期望改善代码质量,促使程序设计架构更趋合理。说白了,重构解决的就是代码和代码结构的问题,它开始自坏味道,其目标就是要消除坏味道,消除那些“不合我意”的因素,让代码的意图更清晰。
Martin在《重构》一书中提到了22个常见的代码坏味道,都可以作为我们重构的目标,来指引我们的重构。如:
消除同一类两个方法之间的重复代码
消除某一类中的长方法
重命名
删除A类中的死代码
简化复杂的条件语句
同时,重构的范围也应是那段坏味道的代码,在重构过程中对其,也仅对其进行修改。
小菜:我明白了。这一段代码其实我就是想先去除重复问题的,结果改着改着就改到别的地方了。
2.不知道什么时候完工
经理,我先改上50块钱的,你看行不行?
重构是整理代码保持轻装前行的重要手段,然而我们也需要能够明确知道重构要做什么,最终的产出如何验证。总不能对项目经理说,我先改上50块钱的?
上文提到了消除复杂条件语句是这次重构的目标,那么简化22行-32行复杂的条件语句就是一个更具体的重构目标。有了这样一个具体清晰的目标,“重构什么时候停”也就是一个很容易回答的问题了,不用担心项目经理天天问你啥时候完工了。
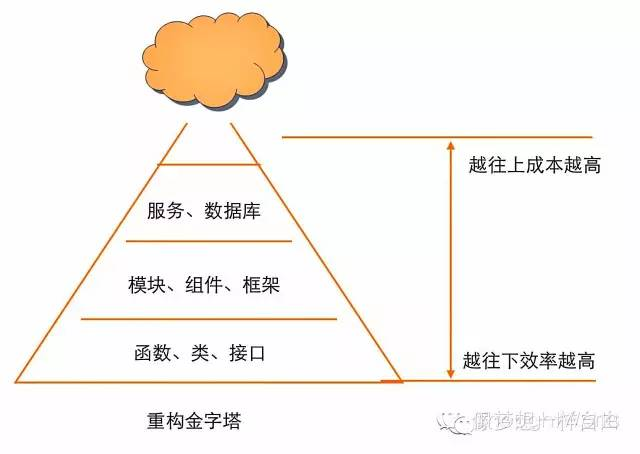
重构其实不仅有代码级别的重构,还包括模块级别的重构、架构级别的重构。不同级别的复杂度不同,消除的坏味道不同,需要的时间也不同。一般来讲代码级别的重构可以在小时和天以内,架构级别需要的时间会更长一些,比如几周或几月或几年。
3.没有方法,暴力重构
“非常的建设需要非常的破坏。”
很多人都认同这一观点。但对遗留的应用软件、构筑过半的项目却容不得推倒重来。以我观察,在开始重构时仅凭自己对代码的理解就进行剪切、复制、删除、添加等大刀阔斧修改的人不在少数,尤其还没有完全掌握重构手法的新人们。结果当然错误百出,导致测试“奖赏”一片红。修复这些错误代码少则几个小时,多则几天,这不是重构,这是重写。
小菜:那怎么破呢?
无他,苦练而已。
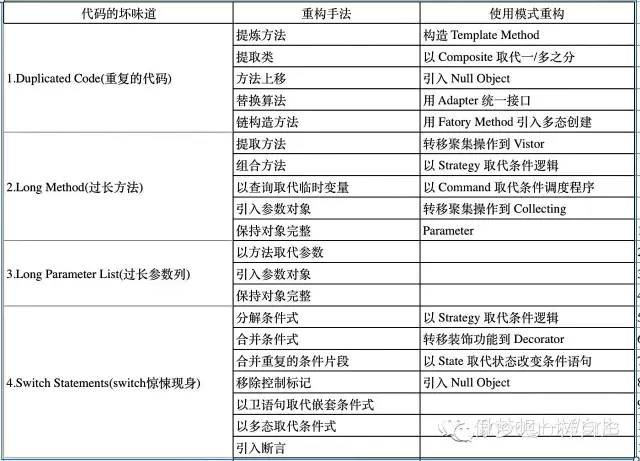
重构是一种经千锤百炼形成的有条不紊的程序整理方法。在《重构》一书中Martin明确提出了68个代码级别的重构手法,这些手法都是等价的。在重构的过程中即使错了也没关系,都可以安全回退,重新开始。其中比较常用的手法就是桥接,如当我们要删除一个方法的时候,会新添加一个方法,然后将它的引用逐一的迁移过去,直到旧方法成为孤岛,就可以将它删除了。它能保证重构前与重构后的程序代码功能完全一致,从而实现安全重构。
所以小菜啊,这是20个招式,回去加紧练习啊;三月后再来见我。
小菜:是不是就像拳击比赛,不能空有一身蛮力,也得有技巧。
小明:孺子可教也。
4.没有策略,追求完美主义
重构过程中,经常出现为了消除一个坏味道,改了A类的方法,又改了B类的变量,不得不改了C类;最后发现这三者之间还有依赖,导致进行不下去了,波及面越来越广,时间越来越长,项目经理在催,最后不得不放弃所有的代码。
老子说:“治大国,如烹小鲜。”
调整一个正在运行中的系统也如治国,不要期望一次性调整到漂亮的代码或架构,而是要遵循“小步前进”的方法。从问题着手,每次重构一小步。针对一个问题有目的修改,修改完后测试,测试通过后提交代码,再进入下一轮重构。如果在改动过程中发现了其他需要修改的地方,不要顺便重构,你可以把它记下来,作为下一轮重构的内容。
这种做法在代码和模块层面都是相对比较容易实践,而针对架构层次的调整就相对比较复杂。这也是很多架构师需要去思考的问题,如何渐进式重构。不搞一下子半年一年的重构,而是以周以月为单位,快速的迭代,能够很快的验证结果获得收益。
5.不知道结果对不对
对于简单的代码级别重构如果做得好是可以不用验证结果的,然对于模块级别或架构级别的重构,是需要的。在我遇到的多次重构架构失败的例子中,很多是因为越做越发现很难验证结果的正确性,越做越不知道改的对不对,最后发现很难回答老板和客户的问题不得不失败。
这个时候一个可以衡量重构的指标就体现它的价值:能时刻检验我们的成果,确认我们的重构还在解决当初的问题。目前常见的量化指标有如下四类,可供参考。
数量:代码的行数
质量:代码复杂度、重复读、缩进等级、架构依赖复杂度等
时间:花费的天数
成本:投资回报率
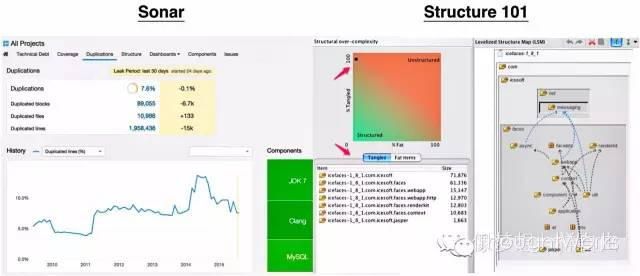
同时也可以借助于Sonar、Structure101这样的一些成熟工具度量和管理这些结果。
6.只谈招式,不谈心法
《重构》是Martin和Kent对他们多年以来整理代码的实践的总结,然这背后体现的是他们对软件技术的深层次思考和经验。很多新人执着于学习重构手法而疏于学习背后的心法,有些可惜。
Robert C Martin的《代码整洁之道》和《敏捷软件开发:原则、模式与实践》、《设计模式》、Eric的《领域驱动设计:软件核心复杂性应对之道》、《架构之美》等都是帮助大家修炼心法的不错选择,他们可以让你更深层的了解代码,更高层面看待系统,锻炼你的嗅觉,提升你的代码能力。
7.不了解上下文,不与团队沟通
我们不得不承认对代码的重构是有风险的,尤其是模块或架构级别。这段代码的业务是什么,为什么当时这么设计,测试覆盖率是多少,如果这样改会不会影响到其他模块?对其他角色有什么影响?这些问题都要逐一回答。在风险相对较大的改动更要如此,需要和团队成员,各个角色,包括项目经理和客户进行沟通,谈论这次重构的好处和风险,获得足够的评估,从而能够做出合适的重构决策,将风险降到最低。
今天就聊这些吧。不过小菜啊,你不要担心,重构和做其他事情一样,要有目标有方法有策略有结果。我们在进行的时候需要以终为始,不忘本心。最重要的是要提升技术能力,学习安全重构手法,小步前进,渐进式的重构,不断验证重构的收益,才能迎接一个一个的重构任务,真正的成为清理代码的高手。
加油吧,我看好你哦。